Exploring a Fraud Dataset at a Calling Card Company
Written by Scott W. Strong
In the first part of this series, I discussed how important it is as a data scientist to ask the right questions when solving a new problem. In this post I will be digging into a specific example relating to the situation when a data scientist is presented with data to explore. Specifically, we will be looking a dataset from a calling card company that was experiencing issues with fraud. But first, let’s review the key questions that should be answered when beginning any problem like this one.
- What labels/information is available?
- How do each of the data points impact/influence the system?
- Is the data continuous, discrete, categorical, or a combination?
- What can we gain from the information provided?
- Hypothesize useful information that may results from analysis
- Would additional data be helpful?
- What data isn’t provided that may enhance your insights?
- What can we use to understand the structure of the data?
- Are there basic statistics that would be informative?
- Are there visualization techniques that would reveal structure?
- Graphs, clustering, etc.
Given these key questions, let’s take a stab at finding out how fraud is perpetrated in this calling card company.
First, we need to understand the data points that are provided in the data set. The following is a list of the fields available in our data:
- Source Caller (phone #)
- Destination Called (phone #)
- Call Date and Time
- Call Length
- Fraud Label (No Fraud, Call-shop Fraud, Premium Rate Fraud)
Great! We have listed what is available to us, but what does this mean? In a calling card company, customers will purchase a card with minutes on it. They will use those minutes, typically to call internationally, by calling the company’s hotline. First, they enter a PIN (which they usually just set to the default setting — their phone number), and then type in a destination number to make an outbound call.
This provides an opportunity for two types of fraud to occur. The first is call-shop fraud, where someone steals a physical card and sells it to an unknowing customer. That customer will make calls and use the minutes while the thief makes money from the sale. The second type of fraud is premium rate fraud, where a fraudster will obtain phone numbers of the clients of a calling card company. Using those phone numbers as the PIN (remember that a lot of clients just use the default PIN), the fraudster will call the company’s hotline and put a call through to a premium rate number that the fraudster controls. They will play music over the line, or just leave it silent until all of the minutes are drained, netting them cash from the premium rate call. So what does this data look like in terms of basic statistics?
| Total # of Records | 50,000 | % Premium Rate Fraud | 32% |
| # of Unique Sources | 2,729 | % Call Shop Fraud | 41% |
| # of Unique Destinations | 13,408 | % Genuine (Not Fraud) | 27% |
We can see that there is a ton of fraud happening in this data set and the fraud is coming from fairly few sources. This leads us to wonder if there is any relationship between the source phone numbers and if we can distinguish fraud based on the number itself. To explore this potential insight, we must define a way to compare phone numbers. The first thought is to explore phone number similarities to see if numbers that are “close” to one another have similar characteristics. A distance metric was proposed to illuminate these similarities. Take for example the phone numbers below:
404-908-4485
404-907-4486
404-907-3497
We can see that the second number is most similar to the first and the third number is less similar to the first. Using this distance metric, we visualize the graph of the numbers, only making a connection (an edge) in the graph for highly similar numbers. The following graph (clustering based on density of connections) is what we get for the source numbers.

As we can see, some interesting clusters form simply from the structure and similarity of the phone numbers in this data set. This leads us to wonder if each of these clusters relate to similar labels (call-shop fraud, premium rate fraud, or genuine). Making a small modification to our analysis, we can produce the next chart, which is colored by label (Green – Genuine, Red – Premium rate fraud, and Yellow – Call-shop fraud).
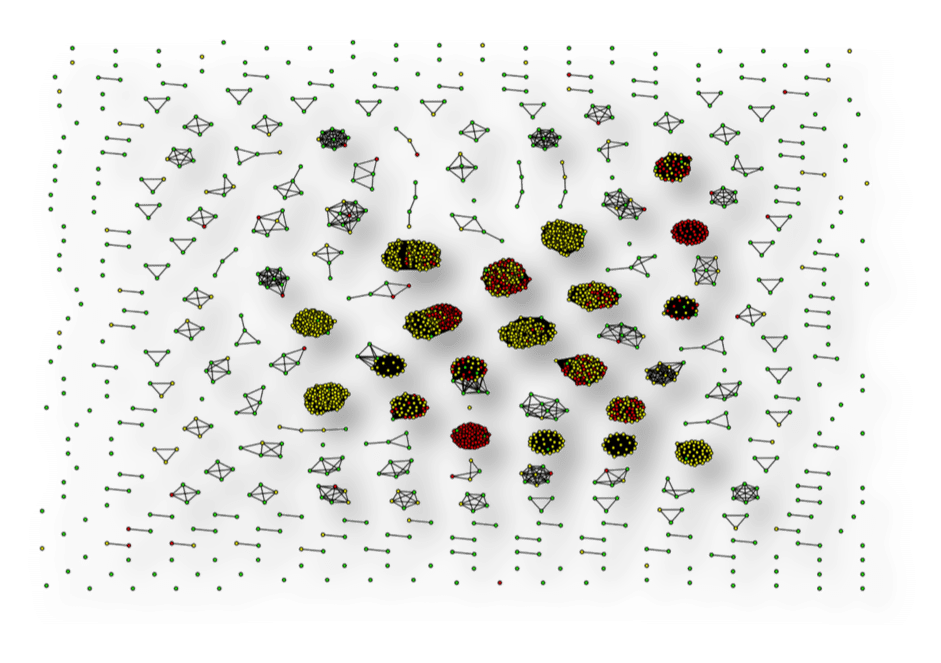
This small change in our analysis has illuminated a huge insight. This colored version of the chart shows us that not only do source phone numbers cluster by similarity in this data set, but the clusters tend to have the same labels. Amazing!
This insight leads us to ask the same question regarding the destination phone numbers. And with some more modifications to the analysis, we can generate the following graph of destination numbers colored by label.

We can see that, even with a much larger set of destination phone numbers, this behavior persists and clusters tend to have the same labels!
Based on this insight, I created features for a simple machine-learning algorithm (random forests in this case) and obtain a 95% true detection rate with only 0.5% false positive rate. It’s crazy (and cool) that we can gain so much information from just the phone number.
Finally, it’s always good to review your results and ask how you can improve your insights. Perhaps we can make more general assertions by including expanding our data set to include service providers or by testing for this behavior in other similar data sets.
In my final post in this series, we will explore the second type of data science problem and I try my hand in predicting the outcome of March Madness. Please feel free to leave your comments below.
Read parts one and three of this series.


